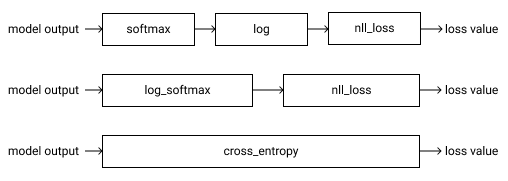
Understanding Cross-Entropy Loss

Recall: a loss function compares the predictions of a model with the correct labels to tell us how well the model is doing, and to help find out how we can update the model's parameters to improve its performance (using gradient descent).

Cross-entropy is a loss function we can use to train a model when the output is one of several classes. For example, we have 10 classes to choose from when trying to predict which number an image of a single digit represents.

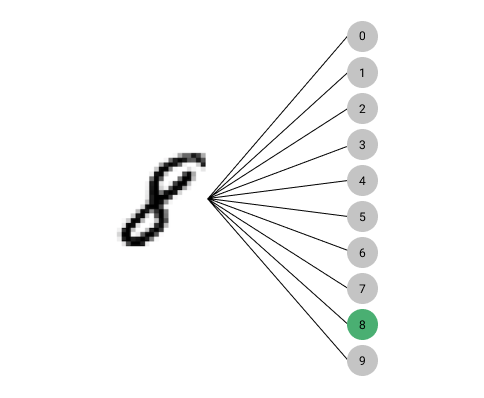
In this image, the number we are trying to predict belongs to the class representing the digit 8.

To use the cross-entropy loss, we need to have as many outputs from our model as the number of possible classes. The cross-entropy loss then enables us to train the model such that the value of the output corresponding to the correct prediction is high, and for the other outputs it is low.

The first step of using the cross-entropy loss function is passing the raw outputs of the model through a softmax layer. A softmax layer squishes all the outputs of the model between 0 and 1. It also ensures that all these values combined add up to 1.

import torch

t = torch.tensor([[-9, 5, 10]], dtype=torch.double)
torch.softmax(t, dim=1)

tensor([[5.5653e-09, 6.6929e-03, 9.9331e-01]], dtype=torch.float64)

Mathematically, each of the values above is calculated as follows:

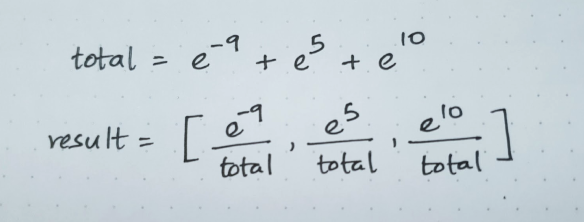
We can create a function to calculate the softmax on our own as follows:

def softmax(x):
  return torch.exp(x) / torch.exp(x).sum()

softmax(t)

tensor([[5.5653e-09, 6.6929e-03, 9.9331e-01]], dtype=torch.float64)

Each value can be interpreted as the confidence with which the model predicts the corresponding output as the correct class.

Since the exponential function is used in the softmax layer, any raw output from the model that is slightly higher than another will be amplified by the softmax layer.

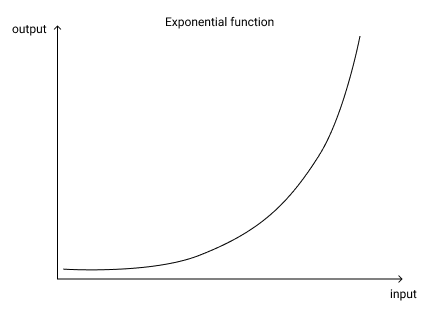
The exponential function amplifies even small differences in input values

This goes to show that the softmax layer tries its best to pick one single value as the correct model output. As a result, this layer works really well when trying to train a classifier that has to pick one correct category.

On the other hand, if you want a model not to pick a class just because it has just a slightly higher output value, it is advisable to use the sigmoid function with each individual output.

After the softmax layer, the second part of the cross-entropy loss is the log likelihood.

By using the softmax layer, we have condensed the value of each output between 0 and 1. This greatly reduces the sensitivity of the model confidence. For example, a prediction of 0.999 can be interpreted as being 10 times more confident than a prediction of 0.99. However, on a softmax scale, the difference between the two values is minuscule - a mere 0.009!

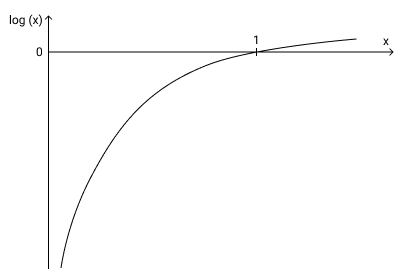
By taking the log of the values, we can amplify even such small differences.

For example,

\frac{0.999}{0.99} \times 100\% = \text{approx. 0.9\% difference in confidence}

However,

\frac{\log{0.999}}{\log{0.99}} \times 100\% = \text{approx. 10\% difference in confidence}

On a log scale, number close to 0 are pushed towards negative infinity and numbers close to 1 are pushed towards 0.

Let us now consider the model output value corresponding to the correct class. If we maximize this value, then all the other values will be automatically minimized (since all values have to add up to 1 because of the softmax layer).

If the output of the model corresponding to the correct class is close to 1, its log value will be close to 0. However, if the model output is close to 0, its log value will be highly negative (close to negative infinity).

We need the value of the loss function to be high when the prediction is incorrect, and low when the prediction is correct. We can have this with the log values if we drop the negative sign (or equivalently, multiply the value by -1). Then, when the model output is close to 0 for the correct class (incorrect prediction), the negative log value will be extremely high and when the model output is close to 1 for the correct class (correct prediction), the negative log value will be close to 0.

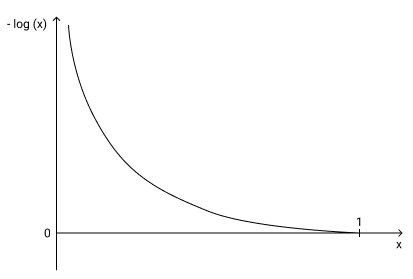
We can then use this as a loss function to maximize the output of the model corresponding to the correct class. Like we saw before, this will automatically minimize the outputs of the other classes because of the softmax function.

This combination of softmax and log-likelihood is the cross-entropy loss.

To see how this all works with PyTorch, let us assume we have 3 data points that can belong to one of 5 classes.

Assume our model produces the following output for these 3 data points:

model_output = torch.randn((3, 5))
model_output

tensor([[-0.7514,  1.2616, -0.4232,  1.3868,  1.2298],
        [ 1.5341, -0.4240,  0.0112, -0.5188,  0.1129],
        [-2.6143,  0.1532,  0.0868, -0.8231,  0.7698]])

Let us also assume that the correct classes for these data points are as follows:

targets = torch.tensor([3, 0, 1])
targets

tensor([3, 0, 1])

We first pass these outputs through a softmax layer:

sm = torch.softmax(model_output, dim = 1)
sm

tensor([[0.0390, 0.2923, 0.0542, 0.3313, 0.2832],
        [0.5784, 0.0816, 0.1261, 0.0742, 0.1396],
        [0.0149, 0.2365, 0.2213, 0.0891, 0.4382]])

As expected, all values have been squished between 0 and 1.

We can also confirm that for each data point, the values sum up to 1:

sm.sum(dim=1)

tensor([1.0000, 1.0000, 1.0000])

Next, we take the log of these values:

lg = torch.log(sm)
lg

tensor([[-3.2429, -1.2300, -2.9147, -1.1048, -1.2618],
        [-0.5476, -2.5056, -2.0705, -2.6004, -1.9687],
        [-4.2092, -1.4417, -1.5081, -2.4180, -0.8251]])

We can then use nll_loss (i.e. Negative Log Likelihood) that will find the mean of the values corresponding to the correct class. This function will also multiply the values by -1 for us before doing so.

import torch.nn.functional as F

loss = F.nll_loss(lg, targets)
loss

tensor(1.0314)

We can manually verify this for the 3 data points:

-1 * (lg[0][targets[0]] + lg[1][targets[1]] + lg[2][targets[2]]) / 3

tensor(1.0314)

Note that the nll_loss function assumes that the log has been taken before the values are passed to the function.

PyTorch has a log_softmax function that combines softmax with log in one step. We can use that function to achieve the same result as follows:

lsm = F.log_softmax(model_output, dim = 1)
loss = F.nll_loss(lsm, targets)
loss

tensor(1.0314)

PyTorch also has a cross-entropy loss that can be used directly on raw model outputs:

F.cross_entropy(model_output, targets)

tensor(1.0314)

The relationship between these three approaches can be summarized as follows:

Understanding Cross-Entropy Loss

References